ROOT-Sim core  3.0.0-rc.2
A General-Purpose Multi-threaded Parallel/Distributed Simulation Library
Macros
heap.h File Reference

Heap datatype. More...

#include <datatypes/array.h>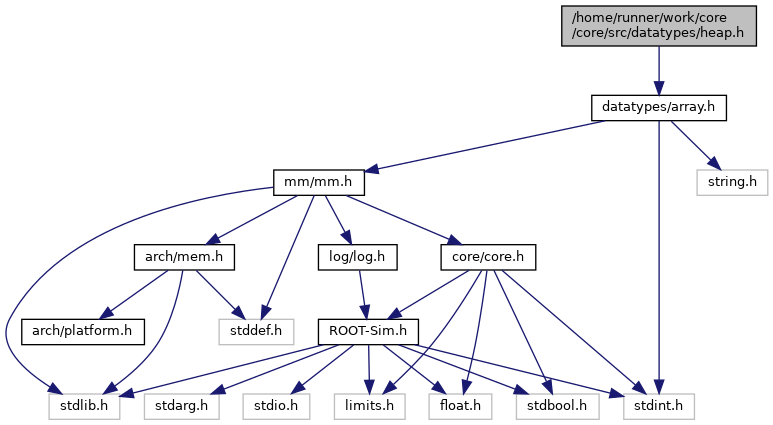
Include dependency graph for heap.h:
This graph shows which files directly or indirectly include this file:

Go to the source code of this file.

Macros

#define heap_declare(type)   dyn_array(type)
 Declares a heap. More...
 
#define heap_items(self)   array_items(self)
 Gets the underlying actual array of elements of a binary heap. More...
 
#define heap_count(self)   array_count(self)
 Gets the count of contained element in a heap. More...
 
#define heap_init(self)   array_init(self)
 Initialize an empty heap. More...
 
#define heap_fini(self)   array_fini(self)
 Finalize a heap. More...
 
#define heap_is_empty(self)   array_is_empty(self)
 Check if a heap is empty. More...
 
#define heap_min(self)   (*(__typeof(*array_items(self)) *const)array_items(self))
 Get the highest priority element. More...
 
#define heap_insert(self, cmp_f, elem)
 Insert an element into the heap. More...
 
#define heap_insert_n(self, cmp_f, ins, n)
 Insert n elements into the heap. More...
 
#define heap_extract(self, cmp_f)
 Extract an element from the heap. More...
 

Detailed Description

Heap datatype.

A very simple binary heap implemented on top of our dynamic array

Copyright
Copyright (C) 2008-2022 HPDCS Group https://hpdcs.github.io

Macro Definition Documentation

◆ heap_count

#define heap_count (   self)    array_count(self)

Gets the count of contained element in a heap.

Parameters
selfthe target heap
Returns
the count of contained elements

◆ heap_declare

#define heap_declare (   type)    dyn_array(type)

Declares a heap.

Parameters
typethe type of the contained elements

◆ heap_extract

#define heap_extract (   self,
  cmp_f 
)
Value:
__extension__({ \
__typeof__(array_items(self)) items = array_items(self); \
__typeof(*array_items(self)) ret = array_items(self)[0]; \
__typeof(*array_items(self)) last = array_pop(self); \
__typeof(array_count(self)) cnt = array_count(self); \
__typeof(array_count(self)) i = 1U; \
__typeof(array_count(self)) j = 0U; \
while(i < cnt) { \
i += i + 1 < cnt && cmp_f(items[i + 1U], items[i]); \
if(!cmp_f(items[i], last)) \
break; \
items[j] = items[i]; \
j = i; \
i = i * 2U + 1U; \
} \
items[j] = last; \
ret; \
})
array_items
#define array_items(self)
Gets the underlying actual array of elements of a dynamic array.
Definition: array.h:41
array_count
#define array_count(self)
Gets the count of contained element in a dynamic array.
Definition: array.h:48
array_pop
#define array_pop(self)
Pop an element from the end of a dynamic array.
Definition: array.h:113

Extract an element from the heap.

Parameters
selfthe heap from where to extract the element
cmp_fa comparing function f(a, b) which returns true iff a < b
Returns
the extracted element

For correct operation of the heap you need to always pass the same cmp_f both for insertion and extraction

◆ heap_fini

#define heap_fini (   self)    array_fini(self)

Finalize a heap.

Parameters
selfthe heap to finalize

The user is responsible for cleaning up the possibly contained items.

◆ heap_init

#define heap_init (   self)    array_init(self)

Initialize an empty heap.

Parameters
selfthe heap to initialize

◆ heap_insert

#define heap_insert (   self,
  cmp_f,
  elem 
)
Value:
__extension__({ \
array_reserve(self, 1); \
__typeof(array_count(self)) i = array_count(self)++; \
__typeof__(array_items(self)) items = array_items(self); \
while(i && cmp_f(elem, items[(i - 1U) / 2U])) { \
items[i] = items[(i - 1U) / 2U]; \
i = (i - 1U) / 2U; \
} \
items[i] = elem; \
i; \
})

Insert an element into the heap.

Parameters
selfthe heap target of the insertion
cmp_fa comparing function f(a, b) which returns true iff a < b
elemthe element to insert
Returns
the position of the inserted element in the underlying array

For correct operation of the heap you need to always pass the same cmp_f, both for insertion and extraction

◆ heap_insert_n

#define heap_insert_n (   self,
  cmp_f,
  ins,
  n 
)
Value:
__extension__({ \
array_reserve(self, n); \
__typeof(array_count(self)) j = n; \
__typeof__(array_items(self)) items = array_items(self); \
while(j--) { \
__typeof(array_count(self)) i = array_count(self)++; \
while(i && cmp_f((ins)[j], items[(i - 1U) / 2U])) { \
items[i] = items[(i - 1U) / 2U]; \
i = (i - 1U) / 2U; \
} \
items[i] = (ins)[j]; \
} \
})

Insert n elements into the heap.

Parameters
selfthe heap target of the insertion
cmp_fa comparing function f(a, b) which returns true iff a < b
insthe set of elements to insert
nthe number of elements in the set
Returns
the position of the inserted element in the underlying array

For correct operation of the heap you need to always pass the same cmp_f, both for insertion and extraction

◆ heap_is_empty

#define heap_is_empty (   self)    array_is_empty(self)

Check if a heap is empty.

Parameters
selfthe heap to check
Returns
true if self heap is empty, false otherwise

◆ heap_items

#define heap_items (   self)    array_items(self)

Gets the underlying actual array of elements of a binary heap.

Parameters
selfthe target heap
Returns
a pointer to the underlying array of elements

You can use the returned array to directly index items, but do it at your own risk!

◆ heap_min

#define heap_min (   self)    (*(__typeof(*array_items(self)) *const)array_items(self))

Get the highest priority element.

Parameters
selfthe heap
Returns
the highest priority element, cast to const
Generated by doxygen 1.9.1